数学が得意な人のイメージ
数学が得意な人のイメージというと、最大公約数的に「有名進学校に通っていて元々地頭の良い、親ガチャも含めて勝ち組の人」ってのがあると思います。
実際にそういう人はいます。数学オリンピックのメダリストなどがそうでしょう。
けれども、それは極一握りです。
実際にはそれぞれそれなりの努力をしています。ここではその一例をご紹介したいと思います。自分のことだと思って読んでください。
やっぱり基本が大事
文字通りです。具体的に言うと教科書です。教科書に書いてある内容をちゃんと理解出来ているかです。余弦定理をちゃんと証明できますか?2次方程式の解の公式を導けますか?メネラウスの定理を使いこなせますか?三角関数の和積公式をちゃんと証明できますか?
 気が遠くなるかもしれませんが、ひとつひとつの公式の意味をまずは理解しましょう。それが出来れば何となく使う場面が想像できそうな感じがします。それを確認するために教科書に載っている問題を解いてください。自力で解いてください。
気が遠くなるかもしれませんが、ひとつひとつの公式の意味をまずは理解しましょう。それが出来れば何となく使う場面が想像できそうな感じがします。それを確認するために教科書に載っている問題を解いてください。自力で解いてください。
どの科目にも言えることですが、特に数学では教科書は最も基本的で最良の参考書であり問題集です。教科書でやる自信がないなら教科書ガイドでやって下さい。解説を読みながら自分で出来るようになっています。
教科書の問題を自力でひと通り、目安の時間で解けるようになったら、数学アレルギーはなくなった、数弱ではなくなったと考えて良いでしょう。
世の中、基本的な事項を問う問題の正答率が8割あれば一人前と見做されたり、一流と見做されたりすることが一般的ですが、数学も同じ。共通テストで8割の得点率というと、東大京大や医学部を除く旧帝大のボーダーラインと考えて良いですが、それが良い例です。
教科書の問題を自力で解けるレベルというのはそのイメージと考えて良いでしょう。
まずはここを目指しましょう。
数学の試験で求められているもの
東大でも京大でも大昔に比べて難問奇問が出題されるケースはかなり減ったなと言うのが正直な感想です。難問奇問の出題されていた時代に要求されていたのは「思考力とスピード」でしたが、そういうのが少なくなった今の時代では「正確さとスピード」です。
まずはここをきっちり理解しなくてはなりません。
勿論、「思考力とスピード」が求められる出題もあるでしょう。その場合は、基本がきっちり出来て、どんなときに何をすれば良いと理解出来ているという意味でパターン化が出来ていれば、たとえ完答できなくても正解にアプローチできるようになっているはずです。そして、それは採点者にも分かるはずであり、確実に部分点をもらえます。
今まで「思考力とスピード」を求められる難問奇問と感じていた問題を「正確さとスピード」を求められている普通の問題と感じられるようになれば、それはそれだけ自分の持っている引き出しが増えたということであり、よく勉強しているということです。
つまり、自分の頭の中でどれだけパターン化出来てるかが数学の出来不出来の指標となります。
「センター惚け」は嘘の時代になりました
センター試験の終わり頃から思っていて、共通テストに衣替えして確信したのですが、「センター惚け」つまり、センター試験対策にかまけていたせいで二次試験に必要な技量が一時的に低下するというのはなくなった、少なくとも昔ほどではなくなったと思います。
というか、そういう勉強をしなければならなくなったと思います。具体的には一つの問題に関して、色んな問題の解き方を理解していなければならないということ、別解をいくつもマスターする勉強をしなければならないということです。
「詰め込みじゃないか」という意見もあると思います。勿論、詰め込みですが、単に暗記するというのではなく、それこそ将棋の棋士が今まで対局した棋譜を全部覚えているような感じです。優秀な野球選手がどの場面で打ち取られたか、どんな状況で打たれたかを鮮明に覚えているのと同じようなものです。きっちり問題と向き合って(初めは時間制限のことは余り考えなくて良いかもしれません)、解けなければ悔しいでしょうし、解けてももっと簡単かつ綺麗に解いている人を見れば悔しく思うはずです。その心を大切にして下さい。
そして、そのためには良い友達を持つか、別解を大切にする指導者や参考書・問題集を探してください。
本来的にはアクティブラーニングは数学で生徒が自発的に用いるべき学習法ではないかと思います(ここを参照)。
最後にお土産~例によって東大入試から
20世紀末(多分1999年)に東大の数学の入試問題で和積公式を証明させる問題が出題されました。恐らく大半の受験生は教科書にあるように証明したことだと思います。勿論、それはそれで結構なことです、教科書を理解しているということですから。
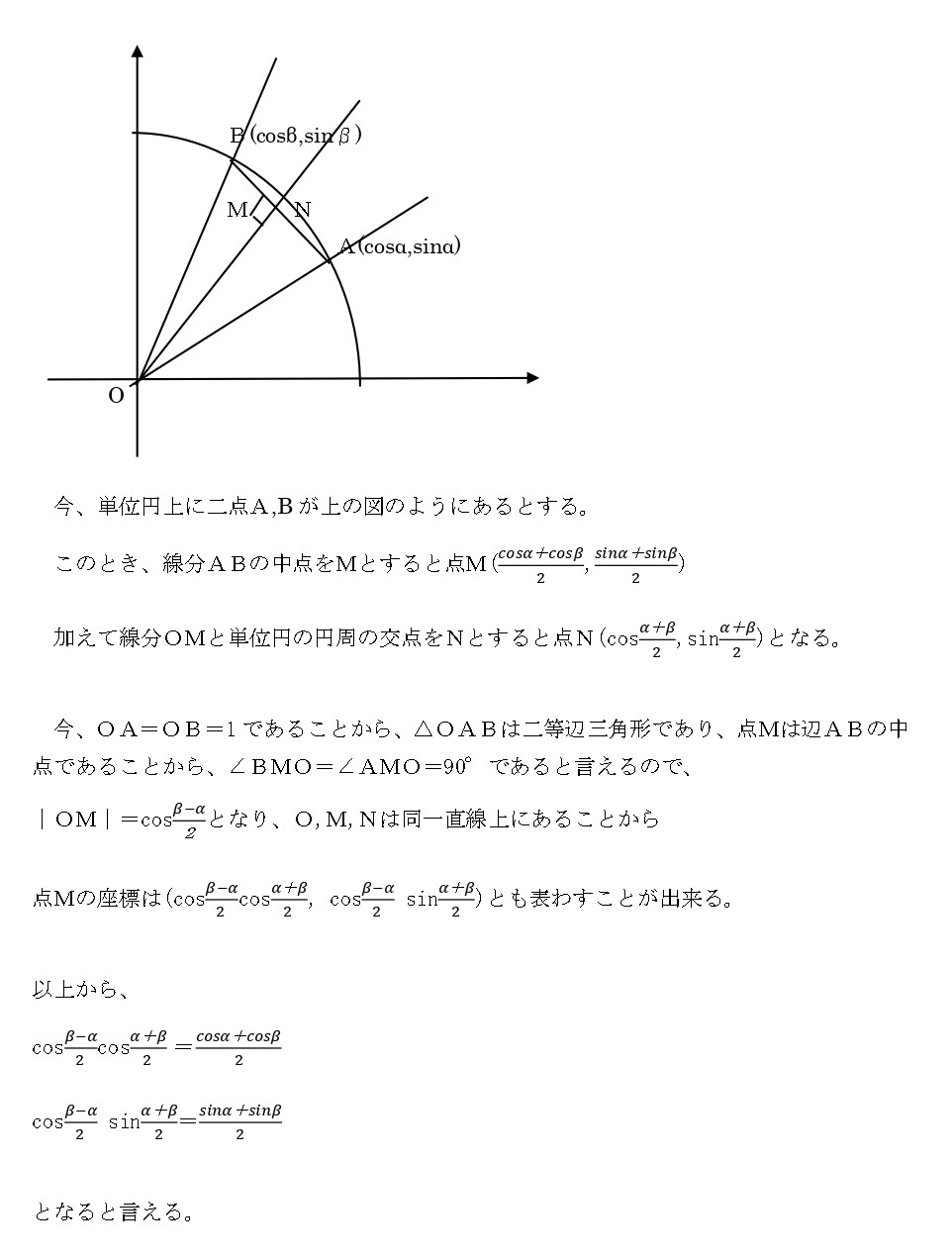 ただ、和積公式の存在意義や何やかんやを考えるならば、こちらにある解法でも良いと思います。これが俗に業界用語(業界=数学の勉強が好きな人の世界)で言うところの「シブい」解き方です。
ただ、和積公式の存在意義や何やかんやを考えるならば、こちらにある解法でも良いと思います。これが俗に業界用語(業界=数学の勉強が好きな人の世界)で言うところの「シブい」解き方です。
如何にも自分オリジナルの解き方かのように偉そうに書いていますが、実はこれ、ある人から教わった解き方です。その人の名前は奥田猛先生(京阪樟葉駅近くにあった盡己塾塾長、ENA、河合塾などで数学を指導)です。
「自然だろ?」といつも仰っていましたが、なかなかその頃は分かりませんでした。最近になって、漸くちょっと自然かなと思えるようになりました。
まだまだ修行せねばならないようです(苦笑)。
